Imgcity

Appearance

Dijkstra Algorithm ​

Source: wikimedia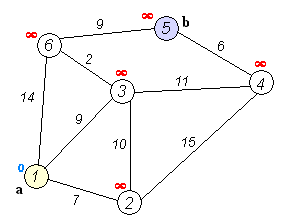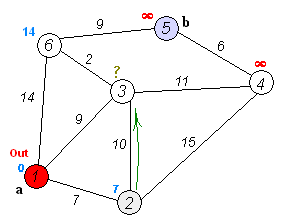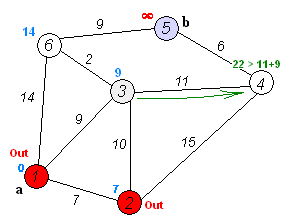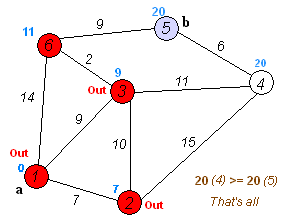

Pseudo Code ​

function Dijkstra(Graph, weight, source) {
  Initial Distances Table (inf if node ≠ source else 0)
  S: Set()
  Q: Queue() Or something that help finding min distance
  Q.Push(source)
  while (!Q.Empty()) {
    u ← Find Min Dist in Queue
    S.Add(u)
    for v adj with u {
      Q.Push(v) if v need to relax
    }
  }
}

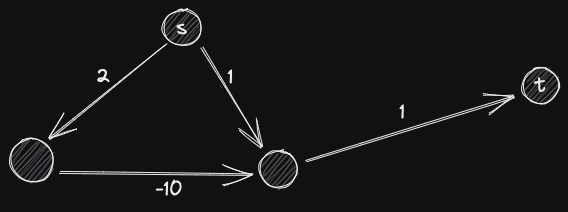
CAUTION

Negative weight may lead to multiple relax time on a same node.

2D Grid ​

Leetcode: 2290. Minimum Obstacle Removal to Reach Corner

cpp
using pii = pair<int, int>;
using pipii = pair<int, pii>;

class Solution {
public:
    int minimumObstacles(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        int inf = 1e5 + 1;

        vector<vector<int>> tab(m, vector<int>(n, inf));
        tab[0][0] = 0;
        
        priority_queue<pipii, vector<pipii>, greater<pipii>> que;
        que.push(pipii(0, pii(0, 0)));
        
        int dets[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
        
        while (!que.empty()) {
            auto [v, p] = que.top();
            auto [x, y] = p;
            que.pop();
                        
            for(int lx = 0;lx < 4;++lx) {
                auto [dx, dy] = dets[lx];
                int nx = x + dx;
                int ny = y + dy;
                if (nx < 0 || nx >= m || ny < 0 || ny >= n) {
                    continue;
                }
                
                if (tab[nx][ny] < inf) {
                    continue;
                }
                
                int nv = v + grid[nx][ny];
                tab[nx][ny] = nv;
                que.push(pipii(nv, pii(nx, ny)));
            }
        }
        
        return tab[m-1][n-1];
    }
};

Changelog

Just observe 👀